The Kepler Problem

New: homework!

Kepler has demonstrated, in chapter 59, that although the planets move in elliptical orbits, it is possible (and actually necessary) to use a circular area to measure the sum of distances of the locations of the planet from the sun, and thus to compute its mean anomaly, or time.

(These images are not transparent, so if you print this page, you'll use up a lot of blue ink. You might be better off copying and printing the text. Click here for a printable version of the diagram from the book.)

Three Anomalies

Here you have the three anomalies, as understood in chapter 59. The eccentric anomaly is the light-blue line along the edge of the path. This measures the angle that the planet has moved from the point of view of the red center. The equated anomaly is the orange arc denoting the angle the planet has moved from the perspective of the sun. The mean anomaly (time) is the sum of the area cut out of the circle by the planet's motion as seen from the sun. It is the red circular sector added to the green triangle.
For Kepler to put his theory into practice, he has to have a way of going from one anomaly to another.

Getting the mean anomaly from the eccentric anomaly

Starting with the eccentric anomaly (blue angle), it is easy to find the mean anomaly (total area -- both red and green). First, create the red sector: as the angle is to the full 360°, so is the area of the sector to the area of the entire circle. Then add the green triangle. Since the area of a triangle is half its base times its height, and the base of the moving triangle is always the eccentricity between the sun and the planet's center, we only have to worry about the height. The dashed blue line measures the height of the triangle, which is the sine of the blue angle. Thus, the triangles are to each other as the sines of the blue angle. So we add the sector, which we know, to the area of the triangle, which we know (using a table of sines to look up the correct height), to get the mean anomaly.
Numerical example:
Let's say the eccentricity is 1/4 the radius, and that the eccentric (blue) angle is 30°. Now, the circular sector is the entire size of the circle (πr² = π, since we can take r as 1) times the portion of the circle we have, or: π × (30°/360°) = π/12. Now, let's take the triangle. It has a base of 1/4 (the eccentricity) and a height of Sin(30°), which is 1/2. So its area is 1/2(base×height) = 1/2×1/4×1/2 = 1/16.
This gives us our total mean anomaly of π/12 + 1/16.

Getting the equated anomaly from the eccentric anomaly

     If arc AK as perceived from the center H is known, then LH is simply its cosine ("sine of its complement" for Kepler). HN is the known eccentricity. Since triangles LHK and THN are similar (sharing the angle at H), as KH is to HL, so is HN to HT. Therefore, we know HT. Now by construction, since it is the way Kepler makes the ellipse, the brown length MN is created equal to KT. Therefore, for triangle MLN, we know MN and LN. So we can simply look up which angle has the cosine of LN/MN, and we'll know the equated angle.
     "Therefore, the angle of the equated anomaly LNM will not be hidden." Numerical example:
Let's again take the eccetricity HN as 1/4, and now make the eccentric angle 60° Now, HK, the radius, is 1, and the cosine LH of 60° is 1/2. Since HK is to LH (1 : 1/2) as HN is to HT (1/4 : HT), this makes HT = 1/8. We can now add HK and HT to get MN = 9/8. We can also add together LH and HN to get LN=3/4.
     Thus, the equated angle we are seeking has as its cosine LN/MN = (3/4)/(9/8) = 2/3. So we look this up in trigonometric table to find that the equated anomaly, angle LNM with cosine 2/3, is 48°11'23".

Getting the eccentric anomaly from the equated anomaly

This one is more difficult! Kepler offers a few methods for this determination, and we will follow his last one, on pages 598-599. Our technique will be to find the length LH, which is the cosine of our desired eccentric angle LHK. We will use radius HK = 1, and eccentricity HN = e.
     First off, we have the angle LNM, and we will look at its cosine: LN = MN Cos LNM. Now LH = LN - HN, so LH = MN Cos LNM - HN, or, since MN = HK + HT = 1 + HT,
     LH = (1 + HT) Cos LNM - e.
But we also know from similar triangles HLK and HTN, that LH:HK=HT:HN, or LH:1=HT:e, which means that
      LH = HT/e.
Combining these, LH = LH, we get:
     HT / e = (1 + HT) Cos LNM - e
Multiplying both sides by e:
     HT = e Cos LNM + e HT Cos LNM - e²
Isolating HT:
     HT (1 - e Cos LNM) = e Cos LNM - e²
Dividing both sides:

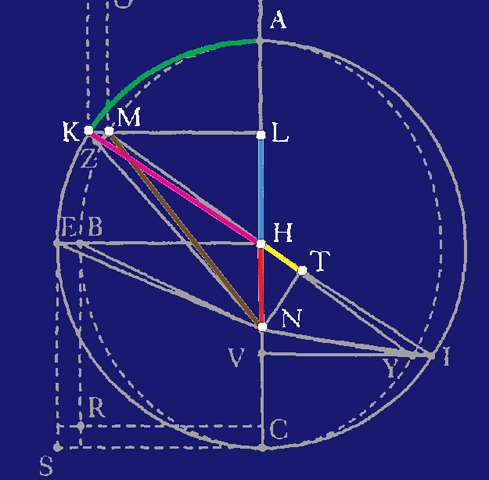
	e Cos LNM - e²
HT =
	1 - e Cos LNM

And since LH = HT / e, we have:

	Cos LNM - e
LH =
	1 - e Cos LNM

So all we have to do is use our correct numbers for the cosine of LNM and our eccentricity e, and we'll have LH. Since LH is the cosine of angle AHK, all we have to do is look it up in a trigonometric table. Numerical example:
Let's use Kepler's example, and take eccentricity HN (e) as .09265, and our equated angle LNM as 30°. We then know that:

	Cos 30° - .09265		.866025 - .09265		.773375
LH =		=		=		=.84084
	1 - .09265 Cos 30°		1 - .09265 .866025		.919763

And, looking up in a table, we see that the angle with cosine .84084 is 32°46', as Kepler gives on page 599.

Getting the eccentric anomaly from the mean anomaly

But given the mean anomaly, there is no geometrical method of proceeding to the equated, that is, to the eccentric anomaly. For the mean anomaly is composed of two areas, a sector and a triangle. And while the former is numbered by the arc of the eccentric, the latter is numbered by the sine of that arc multiplied by the value of the maximum triangle, omitting the last digits. And the ratios between the arcs and their sines are infinite in number. So, when we begin with the sum of the two, we cannot say how great the arc is, and how great its sine, corresponding to this sum, unless we were previously to investigate the area resulting from a given arc; that is, unless you were to have constructed tables and to have worked from them subsequently.
This is my opinion. And insofar as it is seen to lack geometrical beauty, I exhort the geometers to solve me this problem:

Given the area of a part of a semicircle and a point on the diameter [the sun, here], to find the arc and the angle at that point, the sides of which angle, and which arc, encloses the given area. Or, to cut the area of a semicircle in a given ratio from any given point on the diameter.
It is enough for me to believe that I could not solve this a priori, owing to the heterogeneity of the arc and the sine. Anyone who shows me my error and points the way will be for me the great Apollonius. (pp. 600-1)

Numerical example:
Find the eccentric anomaly (blue angle) corresponding to a mean anomaly (combined red and green area) of 1/6. That is, find the eccentric angle corresponding to the planet's location after it has moved one-sixth of the way along its orbit: tell us where it will be in the future. That is the purpose of astronomy, correct? So, work it out -- what's the answer?

Part V